UKIRT
WFCAM - Optical Design
Conceptual
Design Review, August 1999
David Henry
1.
Introduction
This document describes the
optical design for the proposed Wide Field Camera (WFCAM) for the UK Infrared
Telescope (UKIRT). It is presented as part of the conceptual design review
for the instrument.
2.
Specification
The optical system specifications
for the WFCAM are taken from the top level requirements document. Here
we summarise the baseline optical specifications.
- Broad band imaging in J,H
and K bands
- Field of view of 0.93° diameter
- Pixel scale of 0.4 arcsec/pixel
(18µm pixels)
- Image quality of better
than 0.26 arcsecond RMS blur diameter
- Cold stop for K-band imaging
The following wavebands are
assumed for J,H and K.
|
Waveband
|
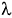 cut-on
(µ m) cut-on
(µ m)
|
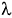 cut-off
(µ m) cut-off
(µ m)
|
|
J
|
1.16
|
1.39
|
|
H
|
1.56
|
1.78
|
|
K
|
2.02
|
2.42
|
3.
Optical Layout & Description
Figure 1 below shows an optical
layout of the WFCAM optical system. Figure 2 shows a close up of the cryostat
optics.
Figure 1
- WFCAM Optical Layout
Figure 2
- WFCAM Cryostat optical layout
WFCAM uses the
existing UKIRT primary mirror (paraboloid, 3.8m diameter, F-ratio f/2.5).
The primary mirror forms the aperture stop for WFCAM.
A new secondary
mirror produces an f/9 focus, at a distance of 5.767 metres in front of
the primary mirror. The secondary mirror is hyperbolic (radius of curvature
-2231mm, conic constant -3.308) and is approximately 472mm in diameter
(approximately 50% larger than the current UKIRT secondary).
At the intermediate
focus, a fused silica field lens is placed. This is used to re-image the
primary mirror onto a convenient cold stop. The field lens is bi-convex
(spherical surfaces), and is approximately 580mm in diameter, by 80mm
thick
The next optical
element is an aspheric corrector plate. This is made from fused silica,
400mm in diameter by 20mm thick. One side of the plate is flat, and the
other side has a weak aspheric profile, similar to a Schmidt plate. This
plate corrects residual aberrations in the system.
The cryostat window
is next. This is a plane parallel fused silica window, of diameter 180mm.
The exact thickness of this window will be determined via an analysis
of the likely vacuum loading, and the need to minimise the resulting deformation
of the surface. This will be the subject of a fuller analysis in the next
phase of the project. The window thickness is likely to be a minimum of
20mm.
Just inside the
cryostat, an image of the primary mirror is produced. The cold stop is
located here.
The tertiary mirror
is located at the rear of the cryostat. This converts the f/9 beam from
the secondary mirror into the f/2.44 beam required to give the correct
pixel scale. The tertiary mirror is a concave hyperboloid (radius of curvature
-1993mm, conic constant -0.0819) of diameter 800mm.
The beam then
passes through the filters - these are discussed in more detail in section
6.
Directly in front
of the focal plane is a fused silica field flattening lens. The lens is
a meniscus, with spherical surfaces. This lens reduces the field curvature
of the system.
Appendix 1 contains
a complete optical prescription for the WFCAM baseline design.
4.
Optical Materials
All of the refractive elements
in the system (field lens, corrector plate, window and field flattener)
are made from fused silica. This is available in various types and grades.
For example, Infrasil 302 from Heraeus provides material with good refractive
index homogeneity, extremely low counts of bubbles and inclusions and
transmission out to 2.5 µm. Fused silica is readily available in
large blank sizes, suitable for fabrication into the lenses required for
WFCAM.
The graph below shows the transmission
of Infrasil 302.
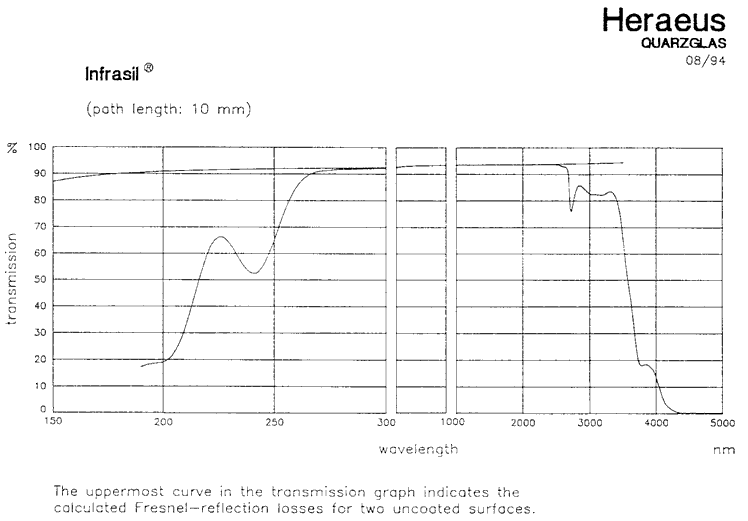
The secondary
mirror will probably be fabricated from Zerodur, similar to the existing
UKIRT secondary mirror. This represents the low risk approach, since the
current secondary mirror is known to perform well.
There are a number
of choices for the substrate material for the tertiary mirror, the main
choices being aluminium alloy, Zerodur and Silicon Carbide. The final
choice of material for this element will be decided by a trade-off study
in the next phase of the project. This study will examine all aspects
of the tertiary mirror (including cost) to arrive at the optimum choice
for the material.
5.
Throughput, transmission and vignetting
Figure 3 below shows the vignetting
(caused by the hole in the primary mirror and the obscuration of the focal
plane) as a function of field angle. The plot is for J band - H and K
band plot are similar.
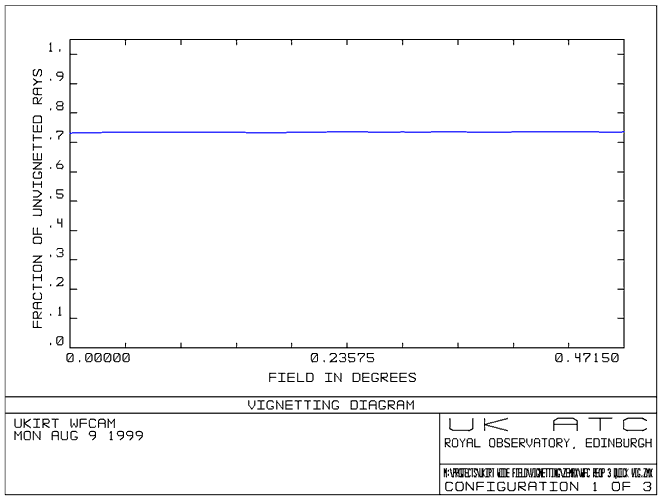
Figure 3
- Vignetting plot
The vignetting
in the system is estimated at around 27%, with little variation across
the field of view.
Tables 1 and 2
below show maximum and minimum estimates of the transmission through the
system.
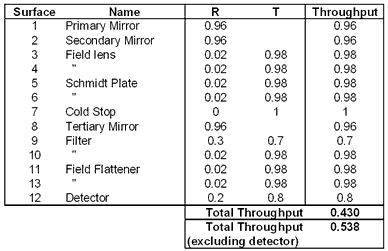 |
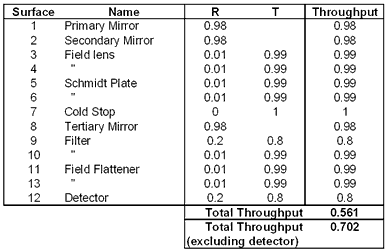 |
|
Table 1 - Maximum transmission estimate
|
Table 2 - Minimum transmission estimate
|
The maximum transmission
estimate is based on 98% reflectivity for mirrors, 1% reflectivity for
lenses and 80% transmission for the filters. Minimum transmission assumes
96% mirror reflectivity, 2% lens surface reflectivity and 70% filter transmission.
The detector is assumed to have a 20% reflectivity - this is included
as these tables are used in the analysis of ghost imaging - see section
8.
Using these figures
we get an estimate of transmission of between 53.8% and 70.2% (excluding
the detector. Combining this with the 73% from the vignetting analysis
gives an overall throughput of between 39.2% and 51.2%.
6.
Filters
The IR filters are mounted
directly in front of the field flattening lens. This minimises the size
of the filters, thereby minimising the obscuration of the beam. Figure
4 below shows an optical layout of the filters. Figure 5 shows a beam
footprint on the front surface of the filter. Beams are shown from the
four corners of three of the four individual detector arrays (a limitation
in ZEMAX restricts the number of field points to 12, meaning that only
beams from three of the four detectors can be shown).
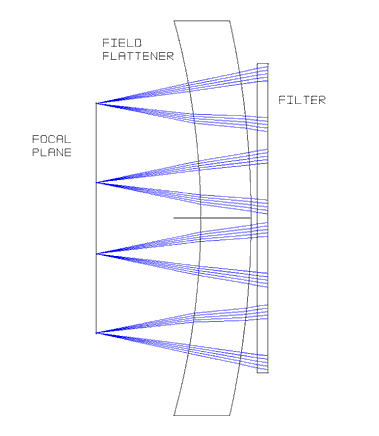
Figure 4
- Filter Optical Layout
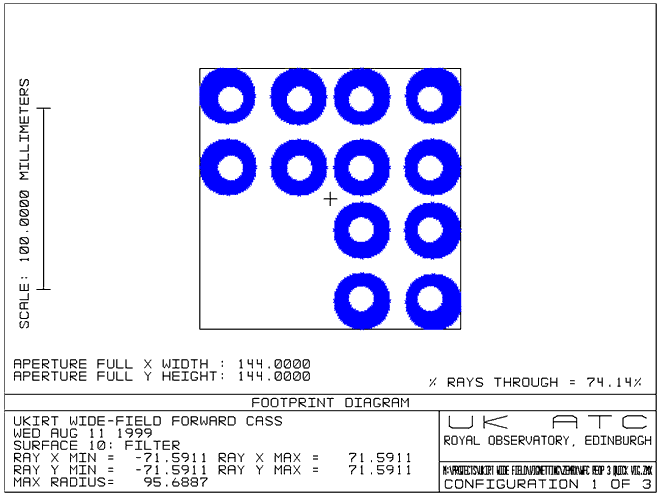
Figure 5
- Beam footprint on filter surface
From the footprint
diagram we can see that the footprints from each individual detector do
not overlap at the filter surface. We can therefore use four separate
filters mounted in a structure to form a 2x2 pattern. This significantly
reduces the manufacturing risk and cost associated with the filters.
For the baseline
preliminary design, each individual filter is approximately 75mm square.
The filters will be fabricated from fused silica, of a similar grade to
that used for the lens elements.
7.
Optical Performance
The plots below show spot diagrams
for the WFCAM system, in J, H and K bands.
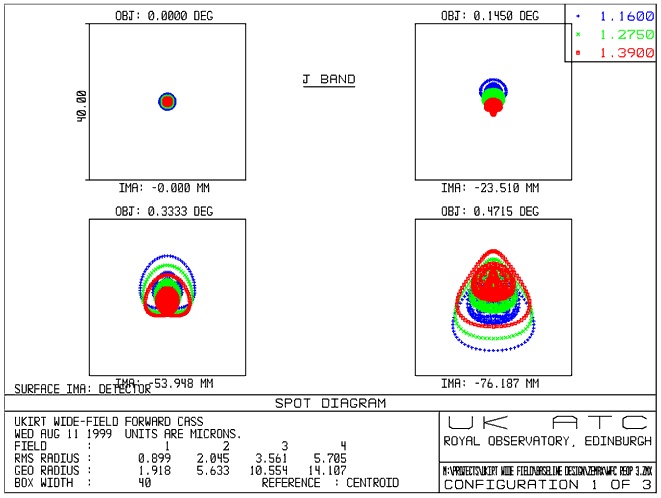
Figure 6
- Spot Diagram (J Band)
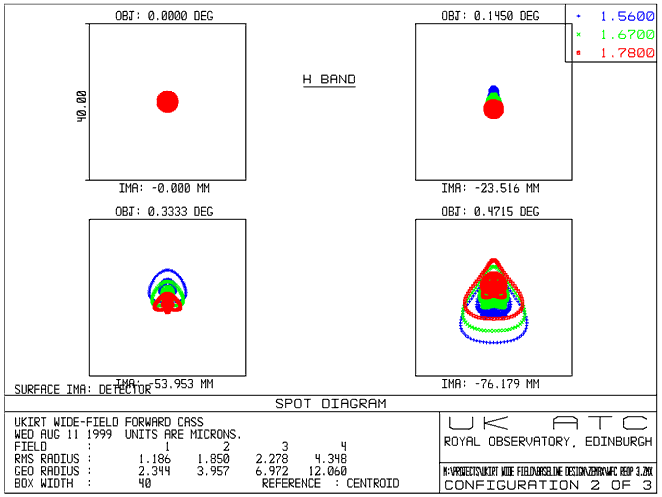
Figure 7
- Spot Diagram (H band)
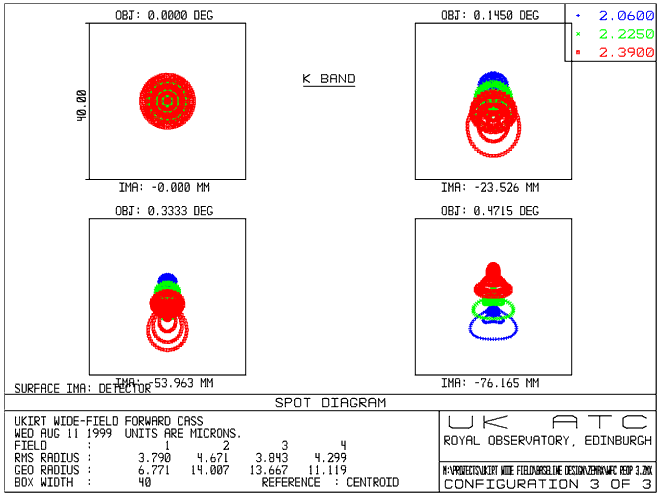
Figure 8
- Spot Diagram (K Band)
The field points
are chosen to represent the inner corner, the edge and the outer corner
of the four detectors (see diagram below). Note that the 0° field position
is not actually imaged by the detector arrays.
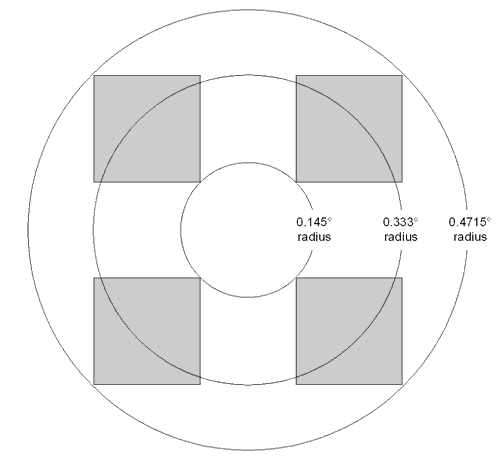
Figure 9
- Focal plane and field of view
The graph below
shows the variation of RMS optical blur diameter (in arcsec) with field
angle for each of J, H and K bands. As can be seen from the graph, the
nominal performance of the system exceeds the specification at all field
angles and wavebands.
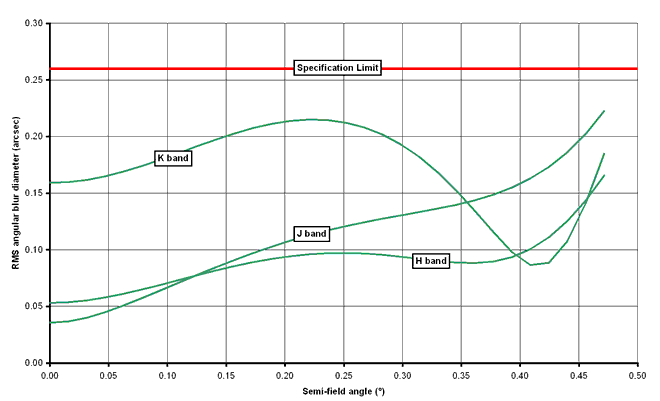
Figure 10
- RMS blur diameter vs. field angle
Note that this
calculation of RMS spot size does not include any diffraction effects.
To get an idea of the effects of diffraction, we can look at the encircled
energy.
The plots below
show the diffraction encircled energy up to a radius of 18mm for J,H and
K wavebands. The calculations are performed on axis, at 0.33° (edge of
field) and at 0.4715° (corner of field). These calculations include the
effects of diffraction from the central hole of the primary mirror and
diffraction from the focal plane.
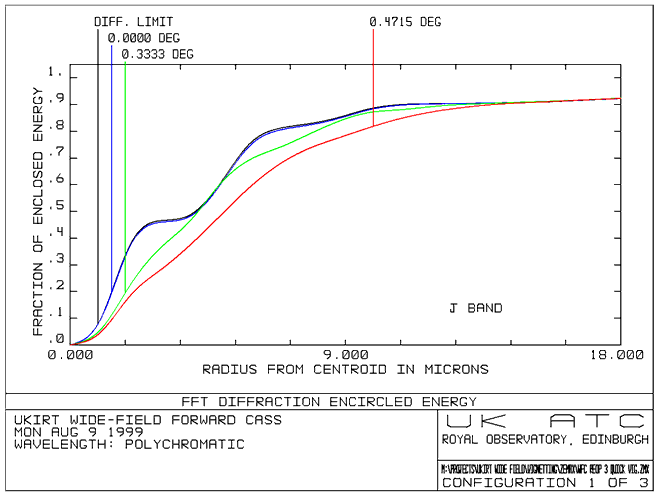
Figure 11
- Encircled Energy (J Band)
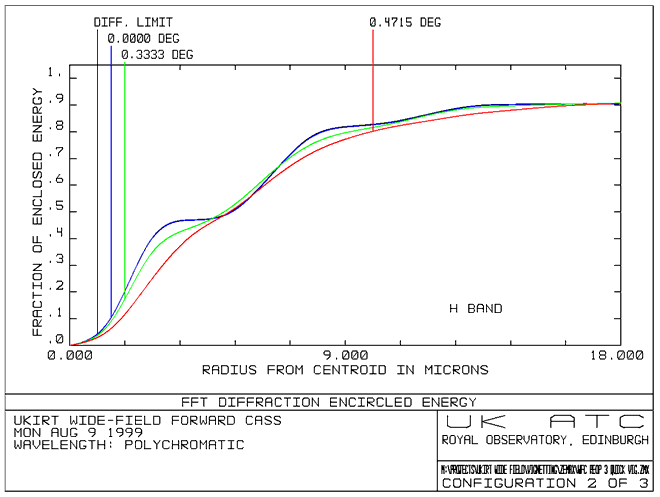
Figure 12
- Encircled Energy (H Band)
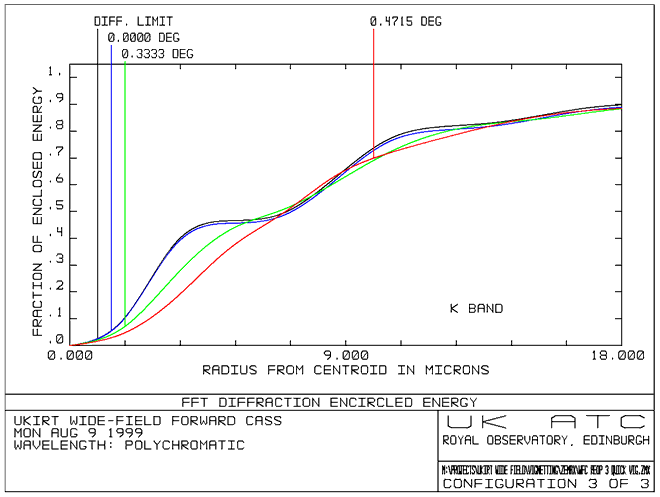
Figure 13
- Encircled Energy (K band)
We can see that
the effects of diffraction are most noticeable at K band.
The plot below
shows the percentage image distortion as a function of field angle for
three wavelengths (which are roughly the central wavelengths for J, H
and K).
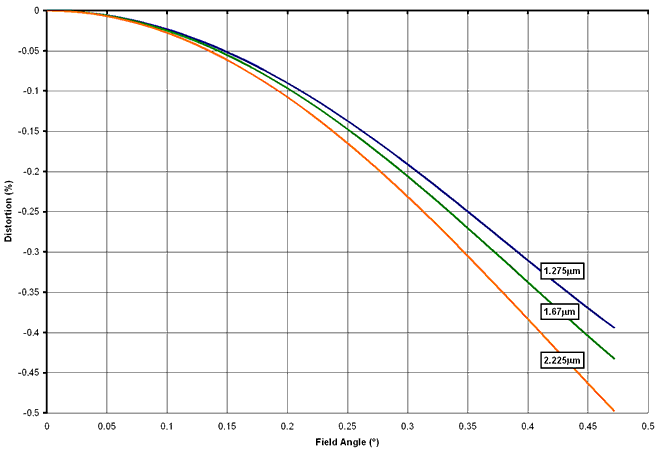
Figure 14
- Image Distortion
The worst case
distortion is 0.5% at the corner of the field of view in K band. This
corresponds to an image shift of 0.762mm, or 42 pixels. Image distortion
will require correction in software when individual frames are "stitched"
together to form an image.
8.
Ghost Imaging
An initial ghost imaging analysis
has been performed. The analysis looked at on axis ghosting only, and
considered double bounces in the system (i.e. light coming in from the
sky is partially reflected from a surface, back towards another surface,
then reflected again towards the focal plane).
The procedure adopted is as
follows.
- A ray tracing analysis is
used to calculate the radius of each of the ghost images on the focal
plane (rghost).
- The area of the ghost image
is then calculated (Aghost).
- The overall transmission
through the complete optical path forming each ghost is then calculated
(Tghost). This takes account of all multiple reflections, and includes
detector reflectivity at 20%. The values used are those shown in Table
1 - Maximum Transmission Estimate in section 5.
- The nominal irradiance in
the ghost image (for an nominal incident power of 1W in the aperture,
and assuming that the power is spread evenly across the defocussed ghost
image) is then calculated as:
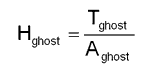
- For comparison, the diffraction
limited irradiance on the focal plane for a point source illuminating
the aperture with a power of 1W is calculated (this is just the peak intensity
for the Airy disk function for a circular aperture). This is calculated
as:
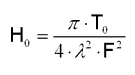
where:
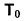 = nominal transmission through system (including detector reflectivity)
= 0.561
= nominal transmission through system (including detector reflectivity)
= 0.561
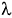 = wavelength = 1.5mm
= wavelength = 1.5mm
F
= optical f-number = 2.44
(Reference - V.N.
Mahajan, "Aberration theory made simple")
- The relative
irradiance of each ghost image is then calculated as 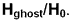
The table below
shows the ghost radius and area, throughput and relative irradiance for
ghost images produced by the surfaces in the system.
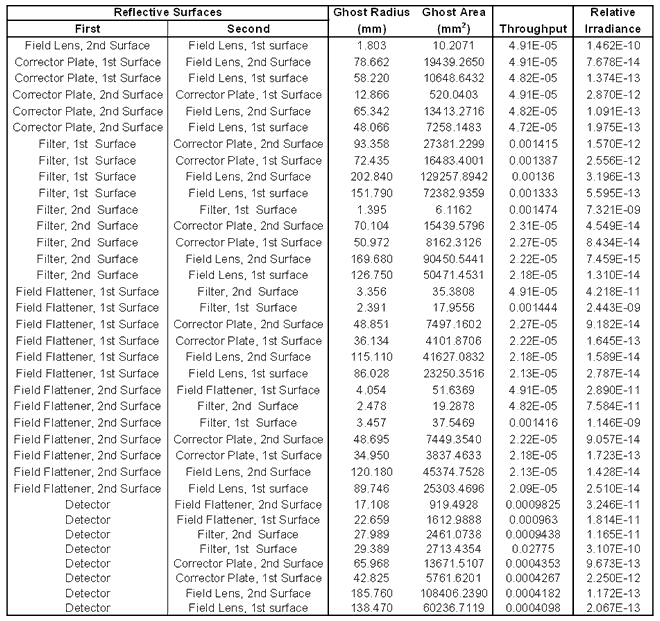
Table 3 -
Ghost Image Analysis
A number of conclusions
can be drawn from this analysis.
- The highest intensity ghost
images are those produced by reflections from the filters, which have
the highest surface reflectivity. However, these are of the order of
109 lower in intensity than the primary image.
- The smallest radius of ghost
image is >1mm in diameter.
- The analysis above was done
using a previous design which did not incorporate a window. Ghost images
from the window are expected to be of the same size and intensity as
those produced by the corrector plate.
- The raytracing analysis
does not correctly handle "second bounces" from the reflective surfaces
in the system (primary mirror, secondary mirror and tertiary mirror).
However, a manual analysis shows that ghost images produced by these
surfaces are highly defocussed. Therefore, these are not included in
the analysis shown above.
In conclusion,
this first order analysis shows that the system should not be susceptible
to ghost imaging, at least to first order. This is mainly a consequence
of the fast F-ratio of the system, which translates into a correspondingly
small depth of focus. This means that ghost images rapidly defocus (and
lose intensity) as the focal point moves away from the focal plane.
In the next phase
of the project, a fuller analysis of all aspects of stray light, including
off-axis ghosting will be carried out.
9.
Tolerancing
An initial tolerance sensitivity
analysis has been carried out on the system.
9.1 Results
of Sensitivity Analysis
Table 4 below shows which parameters
are considered in this analysis, and how the effect in performance is
judged.
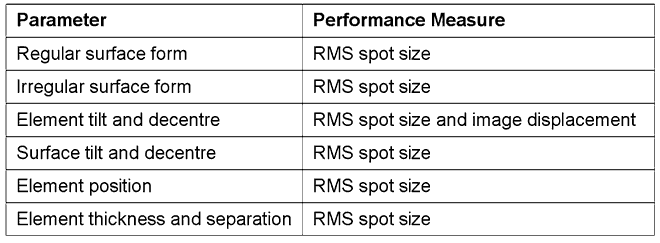
Table 4 -
Tolerance Sensitivity Parameters
Notes:
- RMS spot size is calculated
as the RMS spot radius in microns, on the focal plane. Only geometrical
aberration effects are included.
- RMS spot size is measured
on axis and at a field angle of 0.333° (the edge of the field).
- Highlighted cells in the
sensitivity tables show changes of >0.5% from the nominal value.
- This analysis was performed
with an early version of the design, which did not include the window.
- No analysis has been performed
at this stage of the various aspheric coefficients of the secondary
mirror, the corrector plate and the tertiary mirror.
9.1.1
Regular Surface Form Error
The table below shows the effect
of a change in the regular surface form on the RMS spot size. These correspond
to a change in radius for a spherical surface, or a sphericity on a nominally
flat surface.
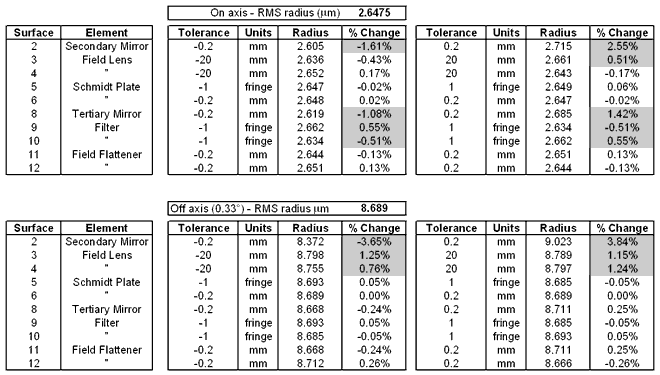
Table 5 -
Sensitivity to Regular Surface Form Error
We can see from
the table that the most sensitive elements are the secondary mirror and
the tertiary mirror. These will require particular attention during the
detailed tolerancing analysis. The field lens is particularly insensitive
(since it is close to a focus) - this is fortunate since the field lens
is large, and therefore difficult to manufacture.
9.1.2
Irregular Surface Form Error
The table below shows the effect
of a change in the irregular surface form error on the RMS spot size.
This can be thought of as departure from sphericity for a nominally spherical
surface (e.g. astigmatism).
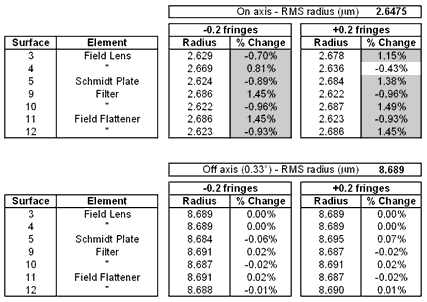
Table 6 -
Sensitivity to irregular surface form error
None of the sensitivities
for irregular form look particularly worrying at this stage. The difficulty
is likely to arise in maintaining these tolerances over the large diameters
of some of the optics.
9.1.3
Element tilt and decentre (image quality)
The table below shows the change
in RMS spot size with element tilt and decentre. These sensitivities correspond
to the mechanical mounting and alignment tolerances.
The "cryostat optics" comprise
the corrector plate, the tertiary mirror, the field flattener and the
focal plane. These are grouped together and acted on as a single element.
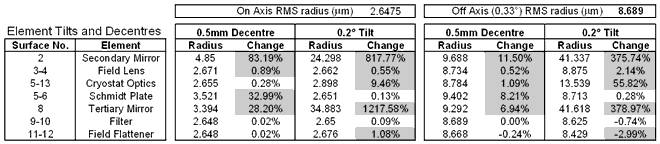
Table 7 -
Sensitivity to element tilts and decentres
We can see that
some of the elements listed are extremely sensitive to tilt and decentre,
which will mean correspondingly tight manufacturing and alignment tolerances.
In particular, the secondary and tertiary mirrors are sensitive to tilt
misalignment.
9.1.4
Element tilt and decentre (image displacement)
The table below shows the image
displacement on the focal plane for small changes in element tilt and
decentre.
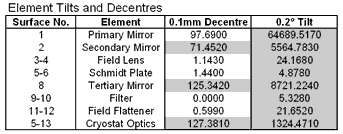
These sensitivities
are useful in determining the likely image motion due to mechanical flexure
of the instrument.
9.1.5
Surface tilts and decentres (image quality)
The table below shows the change
in RMS spot size with surface tilt and decentre. This corresponds to the
wedge angle of a lens, for instance.
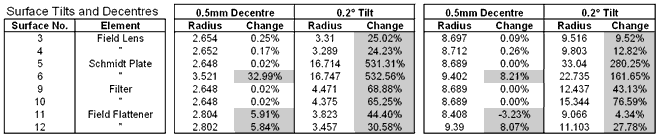
The largest sensitivities
are on the tilt of the corrector plate (Schmidt Plate) surfaces. However,
the wedge angle used for the sensitivity analysis (0.2°) is large when
compared to normal optical fabrication tolerances.
9.1.6
Thickness and Separation
The tables below show the change
in RMS spot size when element thicknesses and element to element spacings
are varied. The analysis is performed with and without back focus compensation.
In addition, in certain cases, thickness compensation is used. This accounts
for the fact that when a lens element is increased in thickness, it will
"expand into" the next air space.
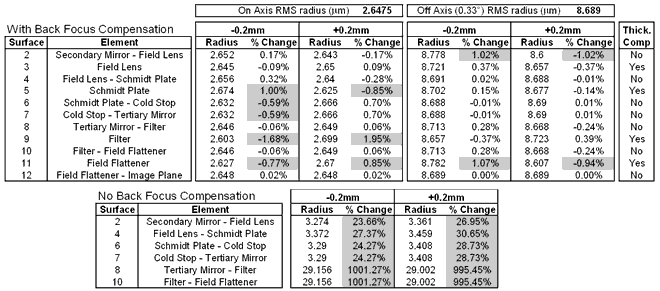
As would be expected,
when the system is not re-focussed, the degradations in image quality
are larger. Using back focus compensation in this analysis is not strictly
correct, since there will be no focus mechanism. However, using back focus
compensation gives us an idea of the amount of one-off adjustment that
will be necessary.
9.1.7
Element Position
The table below shows the change
in RMS spot size when the optical elements are moved by small amounts
along the optical axis. (NB. This differs from the previous analysis which
looked at changes in separation of two elements. Here, compensator surfaces
are used to model the effects of changes in position).

9.2
Key Conclusions from Sensitivity Analysis
The following conclusions can
be drawn from this analysis.
- Some of the alignment tolerances
with regard to tilt and decentre of optical components are highly sensitive.
In particular, the alignment of the primary, secondary and tertiary
mirrors is critical. Due to the large field of view of the system, any
image degradation due to a misalignment of the tertiary mirror relative
to the primary will not be capable of being corrected by movement of
the secondary mirror. Therefore, these three mirrors will require to
be co-axial to an extremely small tolerance.
- Maintaining the precise
optical tolerances likely to be required for the large refractive elements
in the system (field lens, field flattener and corrector plate) is of
concern, and will require particular attention at the detailed design
phase.
9.3
Procedure for detailed tolerance analysis
The following procedure will
be adopted for the detailed optical tolerancing analysis.
- A more detailed specification
of the optical performance requirements will be established. This will
allow effects of diffraction and geometrical aberration to be more easily
combined. For example, a specification based on 50% and 90% encircled
energy diameter would allow more comprehensive analysis.
- The sensitivity analysis
will be repeated for the revised specification. This will include physically
correct compensations (e.g. focussing and alignment using the secondary
mirror hexapod mechanism). The analysis will also be expanded to include
the aspheric components of the system.
- Using this more detailed
sensitivity analysis, and in conjunction with the mechanical engineer,
an initial set of optical and opto-mechanical tolerances will be established.
- Using these tolerances,
a Monte Carlo tolerancing simulation of the optical system will be carried
out. This will yield statistical information regarding the likely performance
of the final system as built, in terms of performance distributions
and confidence limits.
- The results of the Monte
Carlo analysis will be compared with the specification limits. Individual
tolerances can then be refined accordingly.
- The tolerance analysis is
then repeated as necessary until the design meets the requirements.
By following this process,
we should arrive at a design which meets the overall requirements but
which does not contain excessively tight tolerances.
10.
Test and Alignment
A number of areas of the design
may cause particular problems for testing and alignment, and have had
preliminary analyses carried out at this stage.
10.1
Corrector plate and tertiary mirror testing
The aspheric corrector plate
and tertiary mirror are difficult to test using normal optical testing
methods. An alternative is to design a null lens that will allow these
components to be made and tested together. This null lens can also be
used to aid alignment of the optics in the instrument.
The diagram below shows the
test set-up.
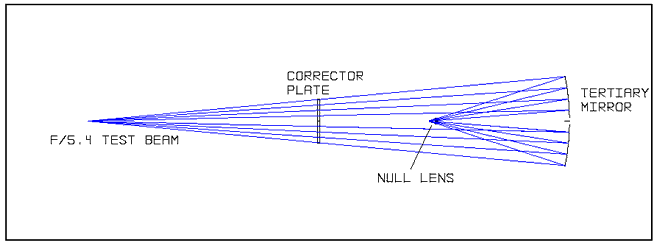
Figure 15
- Null Lens test setup
The test set-up
uses a f/5.4 beam; this completely fills both the Corrector plate and
the Tertiary Mirror. The source is at a distance of 2.1m from the Corrector
plate, which ensures that the elements are tested at the same conjugate
ratios as in the WFC. The distance from the corrector plate to the tertiary
mirror is 2.278m. The test wavelength is 632.8nm.
The test beam
passes through the Corrector plate and is brought to a focus by the Tertiary
Mirror. Just before the focus, the beam passes through a null lens, which
corrects for the aberrations introduced by the Corrector plate and Tertiary
Mirror. A spherical mirror is placed so that it is concentric with the
focus from the tertiary mirror. This retro-reflects the beam back through
the null lens, off the tertiary mirror, through the corrector plate and
back to the original focus.
The null lens
will obscure the beam and produce vignetting on the Tertiary Mirror. For
the layout above, the obscuration is approximately 70mm diameter on the
tertiary mirror.
The diagram below
shows the null lens in more detail. The null lens consists of two BK7
elements and a spherical mirror.
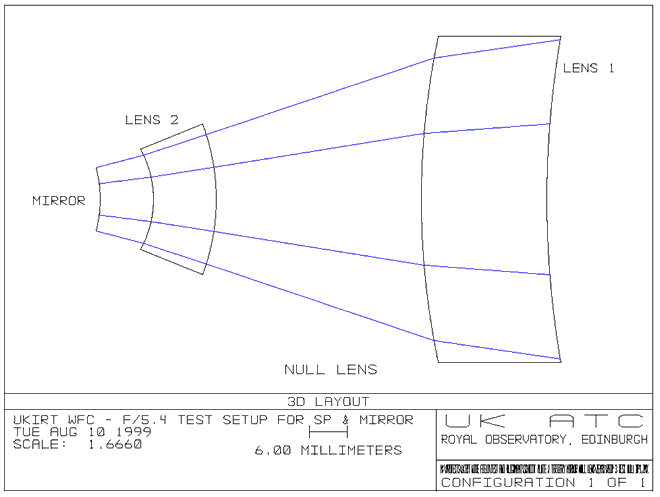
Figure 16
- Detail of null lens
The plot below
shows the double pass OPD through the system. The P-V OPD is 0.0264 and the RMS OPD is 0.0076
and the RMS OPD is 0.0076 . .
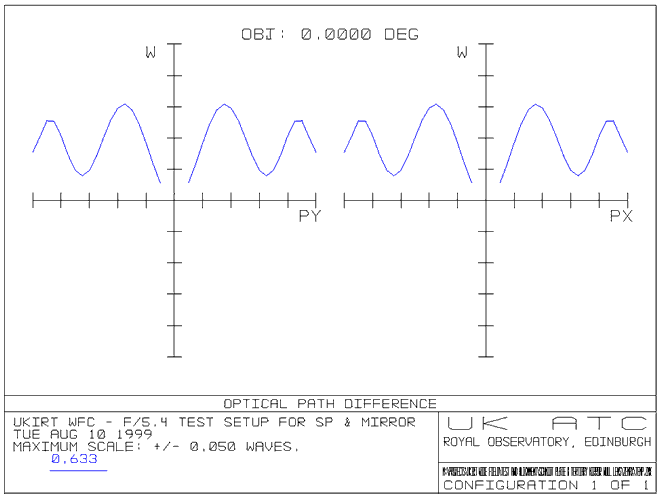
Figure 17
- Null lens performance
10.2
Focal Plane Alignment
Alignment of the four detector
arrays in the focal plane unit is particularly challenging. The tolerance
on co-planarity of the detector arrays is likely to be on the order of
±20mm.
It is likely that each detector
array will be mounted in a cell, which is then machined so that when the
cells are fitted into the focal plane unit, the arrays are co-aligned.
One possible technique is to
use a combination of interferometry and microscopy. The detector active
material (HgCdTe) reflects a reasonable amount of light at 0.633nm. A
parallel beam interferometer could then be used to measure the flatness
of the individual arrays, and the relative tilts between arrays. The tilts
can then be adjusted for on each cell. This leaves the four arrays parallel
to each other, but at different heights. A precision travelling microscope
or optical autocollimator can then be used to measure the height differences
between the arrays.
Appendix A
- Optical Prescription
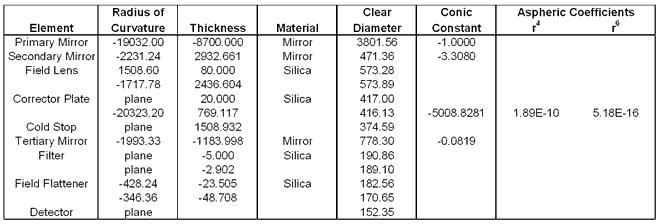
|

